계층적 소프트맥스(Hierarchical Softmax, HS)란?
기존 softmax의 계산량을 현격히 줄인, softmax에 근사시키는 방법론이다. Word2Vec에서 skip-gram방법으로 모델을 훈련시킬 때 네거티브 샘플링(negative sampling) 방법과 함께 쓰인다. 어떤 건지 알아보자. 내용은 유튜브 ChrisMcCormicAI 채널의 설명을 참조했다.
기존 소프트맥스를 Word2Vec에 적용할 때의 문제점
우리가 아는 일반적인 softmax 함수를 MNIST와 같은 간단한 데이터셋에 적용할 때는 문제가 없었다. MNIST는 주어진 그림을 0부터 9까지 분류하는 문제였으므로 output이 10개면 충분했다. 하지만 Word2Vec 훈련 시에는 output의 개수가 Vocabulary에 있는 단어의 개수(적어도 십만 개...)만큼 있고, 십만 번 softmax의 exponential 연산을 수행하는 것은 엄청난 computational cost를 요구한다. 따라서 개선된 방법이 필요했다.
Huffman Tree
Word2Vec에서 vocabulary에 있는 모든 단어들을 잎으로 갖는 Huffman tree를 만든다. Huffman tree는 데이터의 등장 빈도에 따라서 배치하는 깊이가 달라지는 이진 트리이다. Word2Vec에서는, 자주 등장하는 단어(frequent word)는 얕게, 가끔 등장하는 단어(rare word)는 깊게 배치한다.
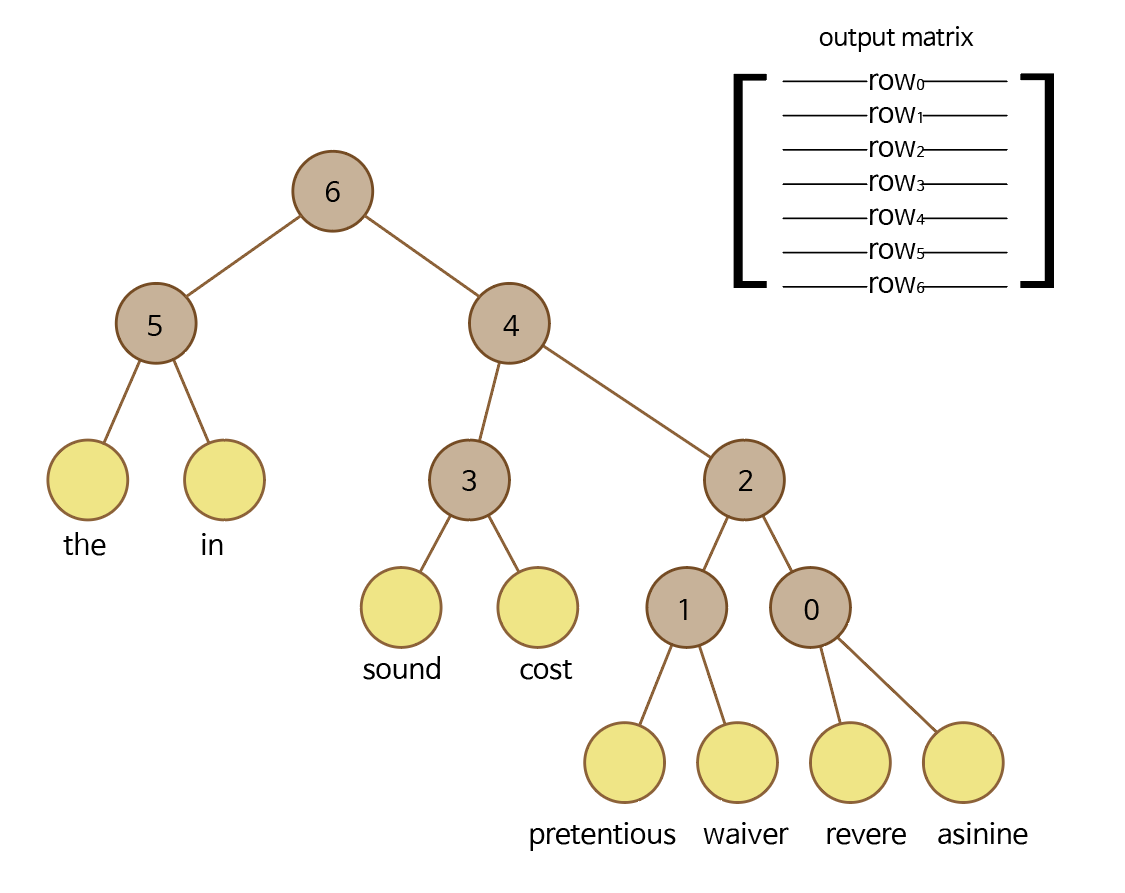
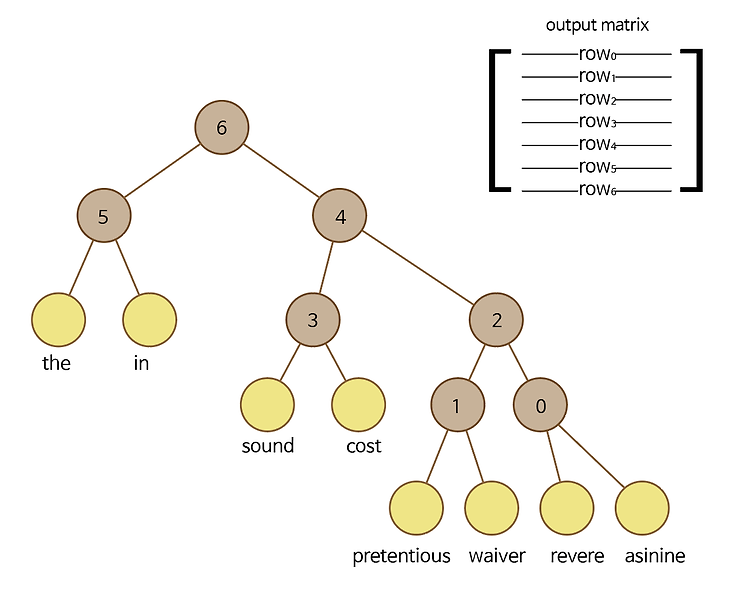
그리고 갈색 노드에 순서대로 번호를 붙인다. 갈색 노드는 내부 노드, 노란색 노드는 단어 노드이다. 내부 노드가 단어 노드보다 1개 적은 것이 이진 트리의 특징이다.
skip-gram에서, 가운데 단어가 asinine이고 문맥의 단어가 cost라고 가정해보자.
그러면, 우리가 원하는 건 asinine을 입력으로 넣었을 때 cost를 출력하도록 가중치를 잘 설정하는 것이다. 이를 어떻게 하는지 알아보자.
맨 먼저, 뿌리 노드(6번 노드)부터 시작한다. asinine 단어의 원-핫 벡터를 6행의 행벡터와 내적한다. 그 값을 sigmoid 함수에 넣는다. sigmoid 함수를 \( \sigma \)라고 하면, \( \sigma (('asinine' ) \cdot (row_6)) \) 을 계산한다.
시그모이드 함수의 출력은 0과 1 사이의 값이다.
계산한 값이 0.24라고 하자. 계산된 값은 6번 노드에서 오른쪽으로 갈 확률이다. 그렇다면 다음과 같은 상황이 된다.
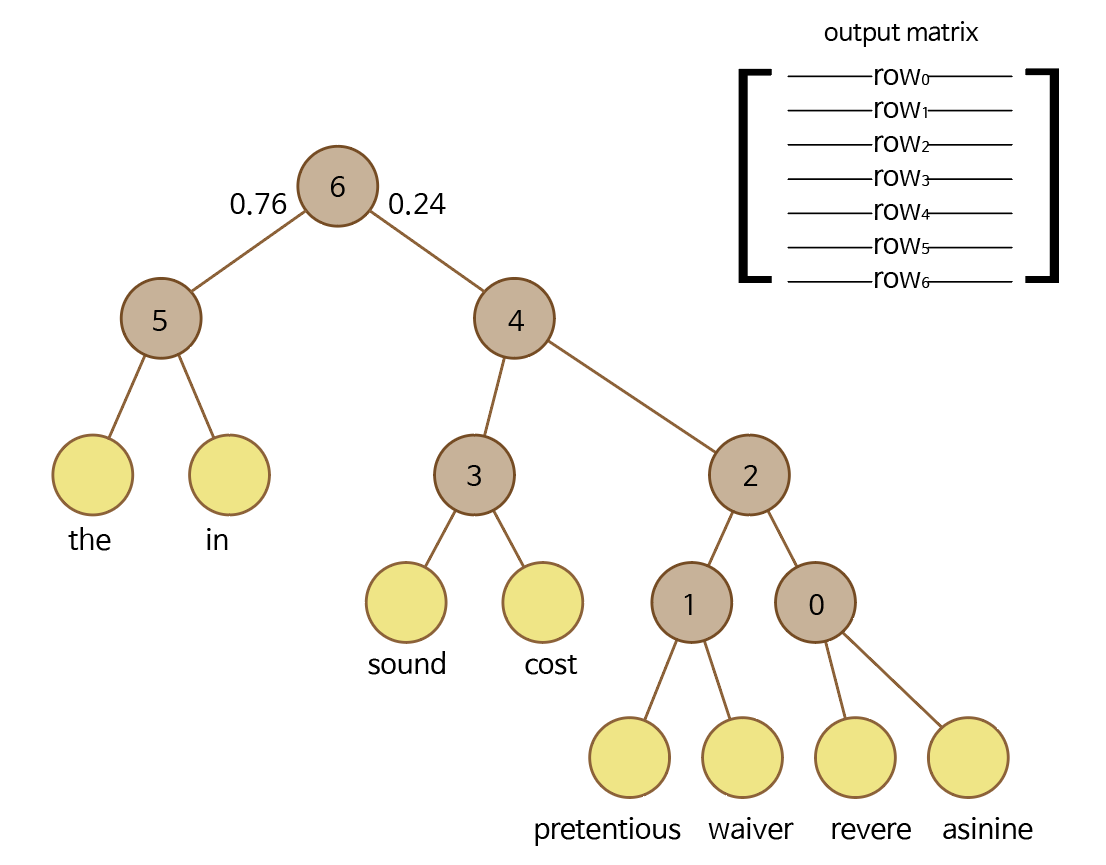
'asinine'단어에 대해서, 뿌리 노드인 6번 노드에서 오른쪽으로 갈 확률은 0.24이고 왼쪽으로 갈 확률은 0.76이다.
이제 4번 노드와 'asinine' 단어 벡터를 계산해야 한다. 마찬가지로 시그모이드 함수를 이용해서 다음을 계산한다. 계산값은 임의로 0.43, 0.68로 정했다.
$$ \sigma (('asinine' ) \cdot (row_4))=0.43 $$
그리고 3번 노드와 내적하면 된다.
$$ \sigma (('asinine' ) \cdot (row_3))=0.68 $$
그러면 다음과 같은 상황이 된다.
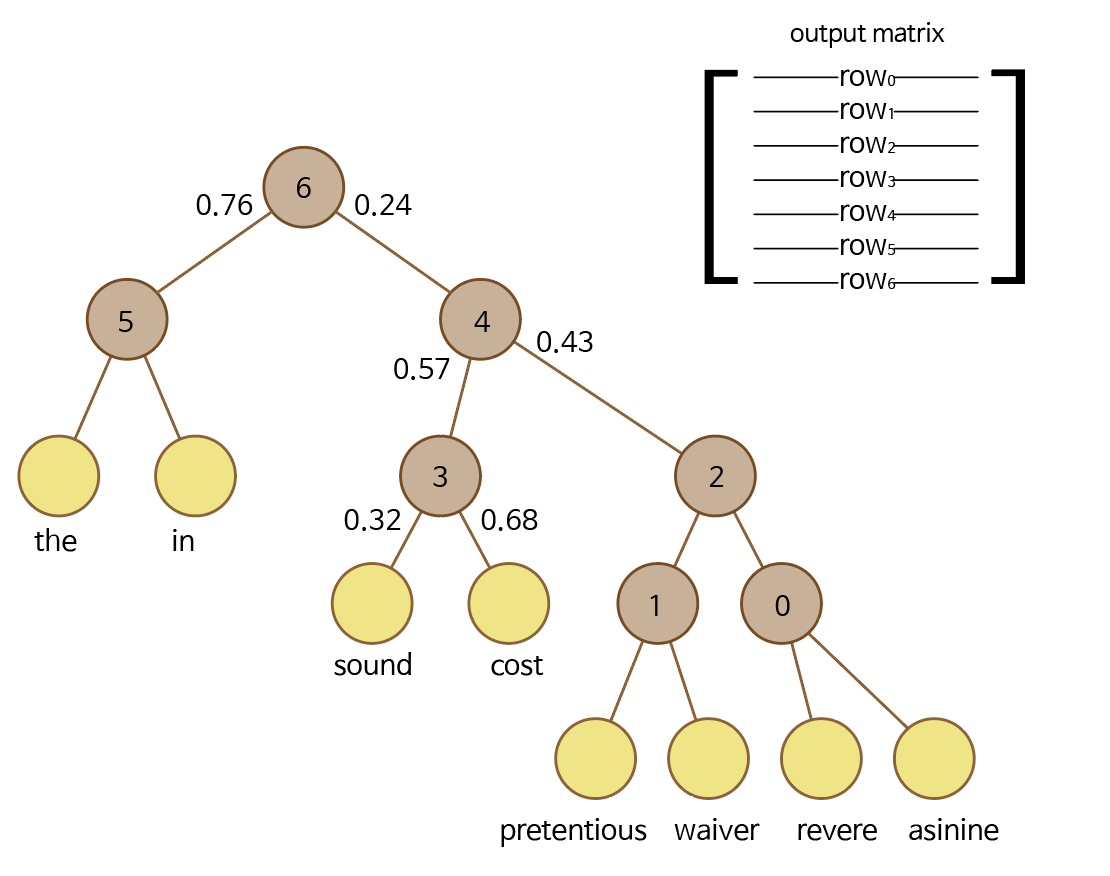
이상이다.
결국, asinine을 입력했을 때 cost를 출력할 확률은 \( 0.24 \times 0.57 \times 0.68=0.09324 \) 이다.
결론
다른 잎 노드에 대해서도 똑같이 계산할 수 있고, 모든 노드에 대해서 확률을 다 더하면 1이 나오므로 확률분포를 이룬다. 이 확률분포를 이용하면 일반적인 소프트맥스처럼 활용할 수 있다.
이진 트리를 사용했으므로, Vocabulary의 크기가 \( V \) 라고 했을 때 밑이 2인 로그를 사용해서 연산량을 \( log_2 V \) 로 줄일 수 있다.
여기서 asinine을 입력으로 받아서 cost를 출력하는 output matrix를 훈련하기 위해서는 6번, 4번과 3번 노드의 가중치만 업데이트하면 된다. 이처럼 연산에 관련된 노드만 훈련하는 것은 negative sampling 방법과 비슷한 특징이다.
'NLP lab > 엔엘피' 카테고리의 다른 글
| ELMo (0) | 2022.03.12 |
|---|---|
| Word2Vec, GloVe, FastText 요약 (0) | 2022.03.12 |
| Context Free Grammar, CYK(CKY) 알고리즘 (2) | 2022.03.01 |
| 오토마타 이론과 형식 언어 (2) | 2022.03.01 |
| 구구조와 의존 구조 분석 (0) | 2022.03.01 |