이 글에서는 로지스틱 함수를 일반화하여 소프트맥스 함수를 유도하는 과정을 살펴봅니다.
읽기 전에 선형 회귀, 로지스틱 회귀와 소프트맥스 함수의 활용에 대해 알아야 합니다.
선형 회귀를 분류에 적용하기
우리가 아는 일반적인 선형 회귀는 다음 그림이다.
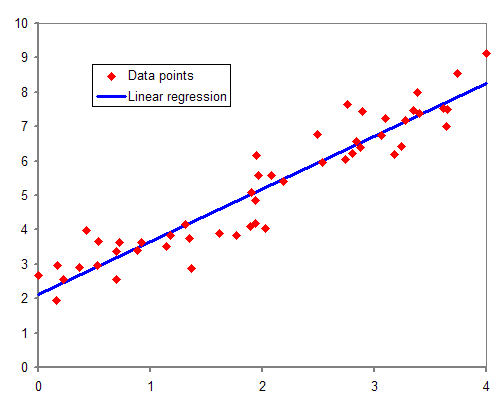
이는 독립변수가 하나일 때의 모형이다. 독립변수가 여러 개일 때의 multiple linear regression의 식은 다음과 같다.
$$ \large{y={\beta}_0+{\beta}_1x_1+...+{\beta}_nx_n} $$
이를 분류(classification)에 활용하기 위해, 간단히 \(y\)를 \(p\)로 바꿔보자.
$$ \large{p={\beta}_0+{\beta}_1x_1+...+{\beta}_nx_n} $$
이 식의 문제점은 \(p\)값이 제한되어있지 않다는 것이다. 확률값으로 만들기 위해 \(p\)값을 0부터 1까지로 제한시키고 싶다. 그래서 우리가 익히 알고 있는 시그모이드 함수를 적용한다.
시그모이드 함수에는 여러 가지(하이퍼볼릭 탄젠트, 아크탄젠트, 에러 함수 등…)가 있지만, 보통은 다음의 로지스틱 함수를 가리킨다.
$$\large{ f(x)=\frac{1}{1+e^{-x}} }$$
로지스틱 함수의 장점은 다음과 같다.
- 실수 전체를 (0, 1)에 매핑시켜 확률처럼 만든다.
- 지수함수를 사용한다. 이는 \(x=0\) 근처에서도 비선형성을 보장한다.
- \(x=0\) 일 때 함숫값이 0.5이다.
따라서 위의 linear combination 식을 로지스틱 함수의 x에 넣으면 다음과 같이 된다.
$$\large{ p=\frac{1}{1+e^{-({\beta}_0+{\beta}_1x+\cdots +{\beta}_nx_n)}} } \tag{1}$$
이로써 선형 회귀식이 이진 분류에 사용 가능해졌다. 만약 위 식의 값이 0.5 이상이면 class A로 분류하고, 0.5 미만이면 class B로 분류하는 등의 규칙을 세우면 되겠다.
오즈(Odds)와 로짓(logit)함수
성공 확률의 실패 확률에 대한 비이다.
$$\large{ \mathrm{Odds}=\frac{p}{1-p} }$$
정리하면,
$$\large{ p=\frac{\mathrm{Odds}}{1+\mathrm{odds}}=\frac{1}{1+\frac{1}{\mathrm{Odds}} } }$$
이다. 이는 식 \((1)\)과 비슷한 꼴이다! 따라서
$$\large{ \mathrm{Odds}=e^{{\beta}_0+{\beta}_1x+\cdots +{\beta}_nx_n }}$$
으로 정의하자. 그리고 지수함수 관계를 선형 관계로 바꾸기 위해 로그를 씌우자. 그러면 로짓 함수를 다음과 같이 정의할 수 있다.
$$ logit(p)=ln(\mathrm{Odds})=ln\left ( \frac{p}{1-p} \right ) $$ $$ ={\beta}_0+{\beta}_1x+\cdots +{\beta}_nx_n $$
로짓 함수는 오즈에 로그를 씌운 것이다. 그리고 이는 로지스틱 함수의 역함수이기도 하다.
로지스틱 함수의 일반화, 소프트맥스 함수
앞서 클래스의 개수가 2개일 때 분류하는 방법을 로지스틱 함수와 함께 알아봤다.
이를 확장하면 우리가 잘 알고 있는 소프트맥스 함수를 유도할 수 있다. 유도 과정은 다음과 같다.
앞서 \({\beta}_0+{\beta}_1x+\cdots +{\beta}_nx_n)\)을 간단히 \(t\)로 놓으면,
이진 분류일 때 오즈는
$$\large{ \mathrm{Odds}=e^t=\frac{P(C_1)}{P(C_2)} }$$
이었다. 이는 \(C_1\), \(C_2\) 클래스가 있을 때 \(C_1\)로 분류될 오즈이다.
확장하여, 클래스의 개수가 \(k\)개일 때, 다음과 같이 세팅한다.
$$ \frac{P(C_i)}{P(C_k)}=e^{z_i} \tag{2}$$
다른 블로그 글을 보면 이 식이 \(C_i\)에 대한 오즈라고 적혀 있어서 헷갈릴 수 있을텐데, 이는 오즈가 아니다. 만약 오즈의 의미라면 분모가 $$P(C_1)+\cdots +P(C_k)-P(C_i)$$가 되어야 할 것이다.
하지만 이는 그저 계산의 편의를 위한 정의다. 그냥 잠깐 이용하는 식이라는 것이다.(사실 이 때문에 글을 작성했다)
예를 들어 위 식에서 \(i=k\)일 때 \(e^{z_k}=1\)이다. 확실히 오즈가 아님을 알 수 있다.
그리고 양변을 \(1\)부터 \(k-1\)까지 더한다.
$$\large{ \sum_{i=1}^{k-1}\frac{P(C_i)}{P(C_k)}=\sum_{i=1}^{k-1}e^{z_i} }$$
$$\large{ \Rightarrow \frac{1-P(C_k)}{P(C_k)}=\sum_{e}^{z_i}e^{z_i} }$$
정리하면,
$$\large{ P(C_k)=\frac{1}{1+\sum{e^{z_i}}} }$$
여기서
$$\large{ 1=\frac{P(C_k)}{P(C_k)}=e^{z_k} }$$
이므로 분모의 1을 바꿔 써주고 시그마 안으로 넣으면,
우리가 아는 소프트맥스 식이 나온다.
$$\large{ P(C_i)=\frac{e^{z_i}}{\sum_{j=1}^{k}e^{z_j}} }$$
'NLP lab > 수학' 카테고리의 다른 글
| 계산 그래프를 활용한 편미분 구하기, 역전파법 이해 (2) | 2022.02.08 |
|---|---|
| 선형대수 복습 (0) | 2022.01.09 |
이 글에서는 로지스틱 함수를 일반화하여 소프트맥스 함수를 유도하는 과정을 살펴봅니다.
읽기 전에 선형 회귀, 로지스틱 회귀와 소프트맥스 함수의 활용에 대해 알아야 합니다.
선형 회귀를 분류에 적용하기
우리가 아는 일반적인 선형 회귀는 다음 그림이다.

이는 독립변수가 하나일 때의 모형이다. 독립변수가 여러 개일 때의 multiple linear regression의 식은 다음과 같다.
$$ \large{y={\beta}_0+{\beta}_1x_1+...+{\beta}_nx_n} $$
이를 분류(classification)에 활용하기 위해, 간단히 \(y\)를 \(p\)로 바꿔보자.
$$ \large{p={\beta}_0+{\beta}_1x_1+...+{\beta}_nx_n} $$
이 식의 문제점은 \(p\)값이 제한되어있지 않다는 것이다. 확률값으로 만들기 위해 \(p\)값을 0부터 1까지로 제한시키고 싶다. 그래서 우리가 익히 알고 있는 시그모이드 함수를 적용한다.
시그모이드 함수에는 여러 가지(하이퍼볼릭 탄젠트, 아크탄젠트, 에러 함수 등…)가 있지만, 보통은 다음의 로지스틱 함수를 가리킨다.
$$\large{ f(x)=\frac{1}{1+e^{-x}} }$$
로지스틱 함수의 장점은 다음과 같다.
- 실수 전체를 (0, 1)에 매핑시켜 확률처럼 만든다.
- 지수함수를 사용한다. 이는 \(x=0\) 근처에서도 비선형성을 보장한다.
- \(x=0\) 일 때 함숫값이 0.5이다.
따라서 위의 linear combination 식을 로지스틱 함수의 x에 넣으면 다음과 같이 된다.
$$\large{ p=\frac{1}{1+e^{-({\beta}_0+{\beta}_1x+\cdots +{\beta}_nx_n)}} } \tag{1}$$
이로써 선형 회귀식이 이진 분류에 사용 가능해졌다. 만약 위 식의 값이 0.5 이상이면 class A로 분류하고, 0.5 미만이면 class B로 분류하는 등의 규칙을 세우면 되겠다.
오즈(Odds)와 로짓(logit)함수
성공 확률의 실패 확률에 대한 비이다.
$$\large{ \mathrm{Odds}=\frac{p}{1-p} }$$
정리하면,
$$\large{ p=\frac{\mathrm{Odds}}{1+\mathrm{odds}}=\frac{1}{1+\frac{1}{\mathrm{Odds}} } }$$
이다. 이는 식 \((1)\)과 비슷한 꼴이다! 따라서
$$\large{ \mathrm{Odds}=e^{{\beta}_0+{\beta}_1x+\cdots +{\beta}_nx_n }}$$
으로 정의하자. 그리고 지수함수 관계를 선형 관계로 바꾸기 위해 로그를 씌우자. 그러면 로짓 함수를 다음과 같이 정의할 수 있다.
$$ logit(p)=ln(\mathrm{Odds})=ln\left ( \frac{p}{1-p} \right ) $$ $$ ={\beta}_0+{\beta}_1x+\cdots +{\beta}_nx_n $$
로짓 함수는 오즈에 로그를 씌운 것이다. 그리고 이는 로지스틱 함수의 역함수이기도 하다.
로지스틱 함수의 일반화, 소프트맥스 함수
앞서 클래스의 개수가 2개일 때 분류하는 방법을 로지스틱 함수와 함께 알아봤다.
이를 확장하면 우리가 잘 알고 있는 소프트맥스 함수를 유도할 수 있다. 유도 과정은 다음과 같다.
앞서 \({\beta}_0+{\beta}_1x+\cdots +{\beta}_nx_n)\)을 간단히 \(t\)로 놓으면,
이진 분류일 때 오즈는
$$\large{ \mathrm{Odds}=e^t=\frac{P(C_1)}{P(C_2)} }$$
이었다. 이는 \(C_1\), \(C_2\) 클래스가 있을 때 \(C_1\)로 분류될 오즈이다.
확장하여, 클래스의 개수가 \(k\)개일 때, 다음과 같이 세팅한다.
$$ \frac{P(C_i)}{P(C_k)}=e^{z_i} \tag{2}$$
다른 블로그 글을 보면 이 식이 \(C_i\)에 대한 오즈라고 적혀 있어서 헷갈릴 수 있을텐데, 이는 오즈가 아니다. 만약 오즈의 의미라면 분모가 $$P(C_1)+\cdots +P(C_k)-P(C_i)$$가 되어야 할 것이다.
하지만 이는 그저 계산의 편의를 위한 정의다. 그냥 잠깐 이용하는 식이라는 것이다.(사실 이 때문에 글을 작성했다)
예를 들어 위 식에서 \(i=k\)일 때 \(e^{z_k}=1\)이다. 확실히 오즈가 아님을 알 수 있다.
그리고 양변을 \(1\)부터 \(k-1\)까지 더한다.
$$\large{ \sum_{i=1}^{k-1}\frac{P(C_i)}{P(C_k)}=\sum_{i=1}^{k-1}e^{z_i} }$$
$$\large{ \Rightarrow \frac{1-P(C_k)}{P(C_k)}=\sum_{e}^{z_i}e^{z_i} }$$
정리하면,
$$\large{ P(C_k)=\frac{1}{1+\sum{e^{z_i}}} }$$
여기서
$$\large{ 1=\frac{P(C_k)}{P(C_k)}=e^{z_k} }$$
이므로 분모의 1을 바꿔 써주고 시그마 안으로 넣으면,
우리가 아는 소프트맥스 식이 나온다.
$$\large{ P(C_i)=\frac{e^{z_i}}{\sum_{j=1}^{k}e^{z_j}} }$$
'NLP lab > 수학' 카테고리의 다른 글
| 계산 그래프를 활용한 편미분 구하기, 역전파법 이해 (2) | 2022.02.08 |
|---|---|
| 선형대수 복습 (0) | 2022.01.09 |
