Transpose property
\( (A+B)^T=A^T+B^T \)
\( (AB)^T=B^TA^T \)
\( (A^{-1})^T=(A^T)^{-1} \)
\( A^T \) is invertable exactly when \(A\) is invertable.
Transpose의 정의 :
세로줄을 가로줄로 바꾸는 행위(X)
모든 \(x\)와 \(y\)에 대해, \((Ax)^Ty=x^T(A^Ty)\)이도록 하는 \(A^T\)를 \(A\)의 transpose라고 한다.(O)
Subspace의 정의 :
다음을 만족하는 벡터들의 집합을 subspace라 한다.
If \(v\) and \(w\) are vectors in the subspace and \(c\) is any scalar, then
(i) \(v+w\) is in the subspace
(ii) \(cv\) is in the subspace.
--- 다음은 2022.02.16에 진행한 세미나로, eigenvector, eigenvalue와 matrix diagonalization에 관해 간략히 요약한 내용을 담고 있습니다.---








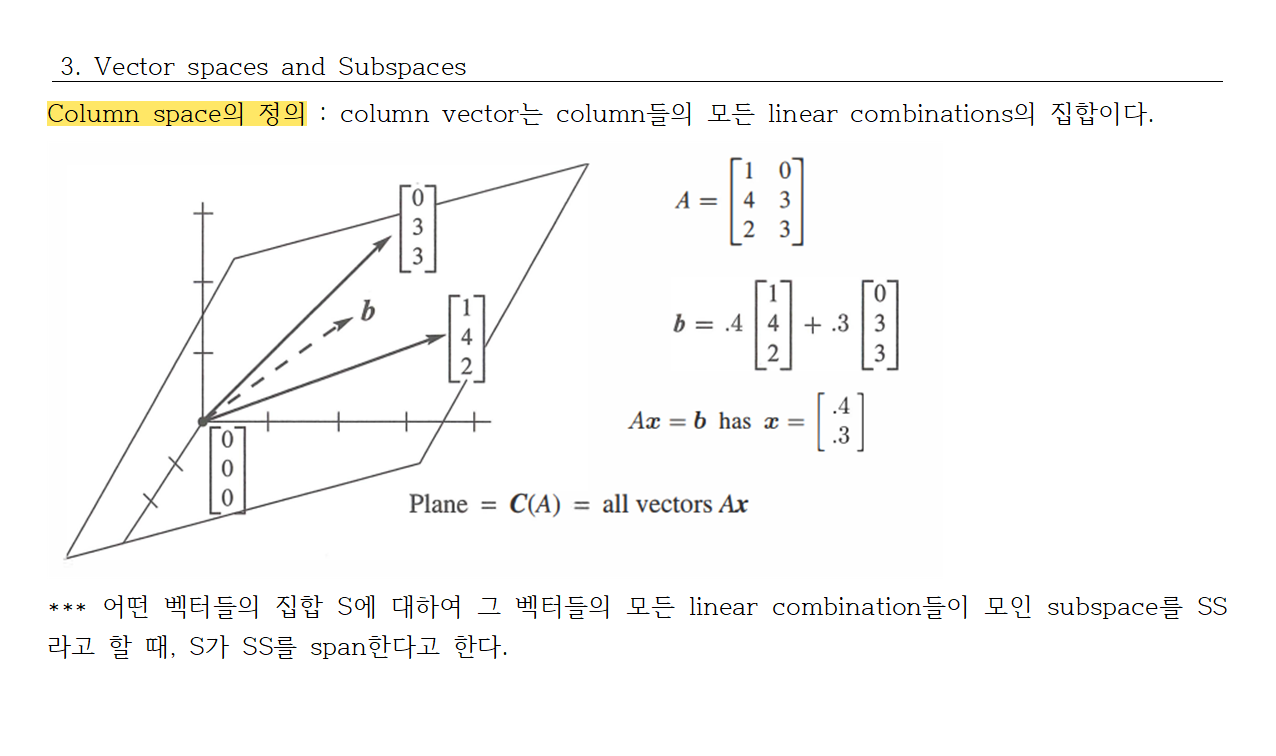





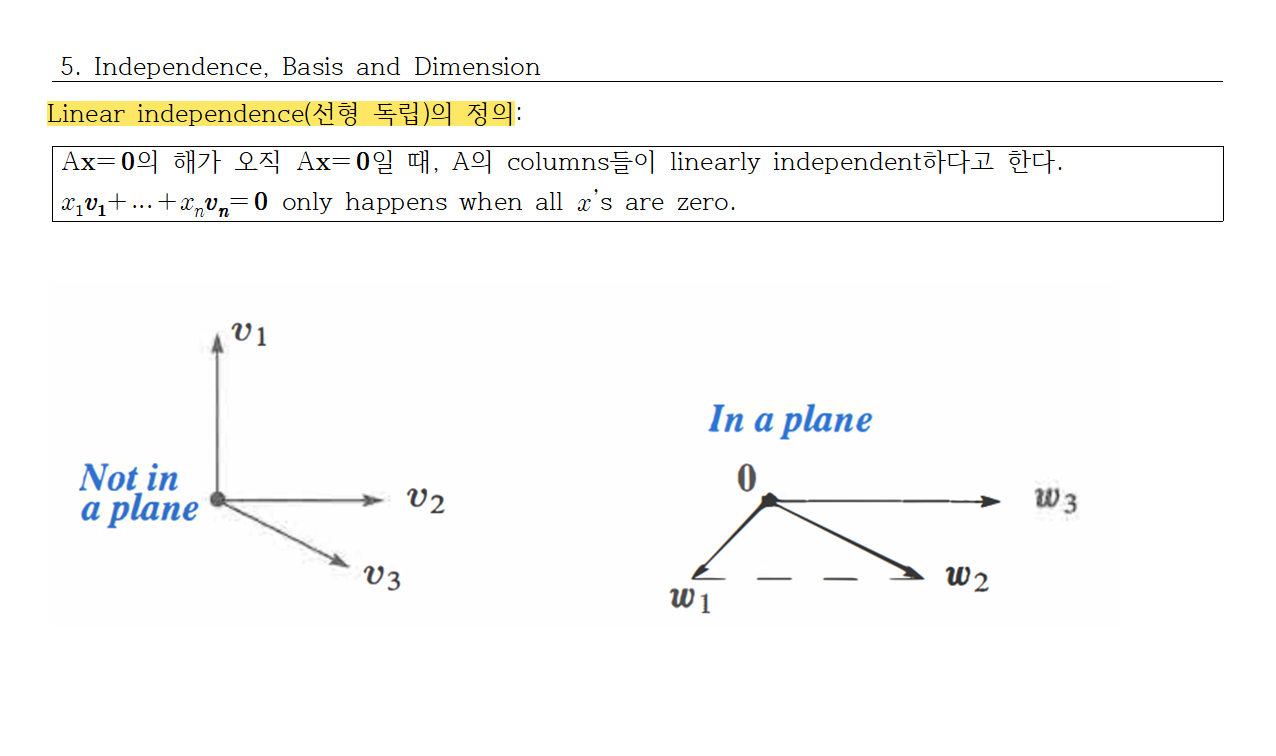



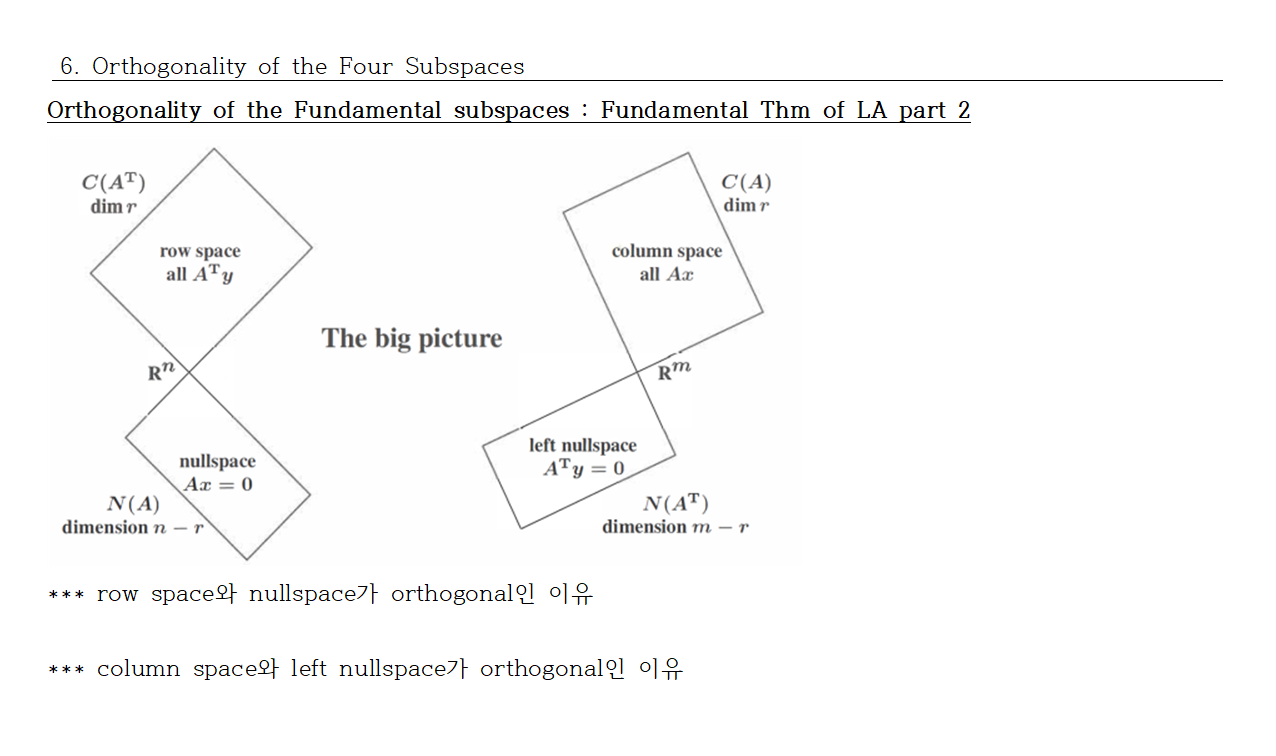
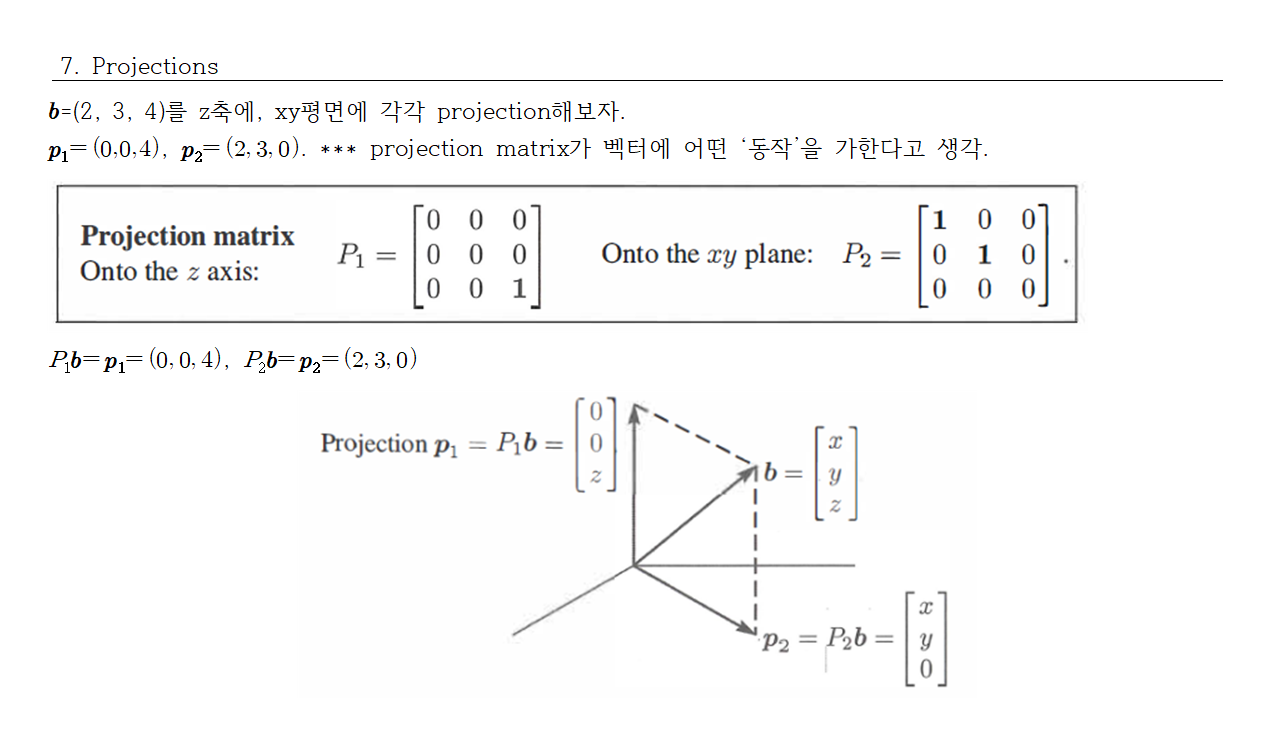












참고 : 길버트 스트랭, 선형대수 입문 5판.
'NLP lab > 수학' 카테고리의 다른 글
| 로지스틱 일반화, 소프트맥스 유도하기 (3) | 2022.05.03 |
|---|---|
| 계산 그래프를 활용한 편미분 구하기, 역전파법 이해 (2) | 2022.02.08 |
Transpose property
\( (A+B)^T=A^T+B^T \)
\( (AB)^T=B^TA^T \)
\( (A^{-1})^T=(A^T)^{-1} \)
\( A^T \) is invertable exactly when \(A\) is invertable.
Transpose의 정의 :
세로줄을 가로줄로 바꾸는 행위(X)
모든 \(x\)와 \(y\)에 대해, \((Ax)^Ty=x^T(A^Ty)\)이도록 하는 \(A^T\)를 \(A\)의 transpose라고 한다.(O)
Subspace의 정의 :
다음을 만족하는 벡터들의 집합을 subspace라 한다.
If \(v\) and \(w\) are vectors in the subspace and \(c\) is any scalar, then
(i) \(v+w\) is in the subspace
(ii) \(cv\) is in the subspace.
--- 다음은 2022.02.16에 진행한 세미나로, eigenvector, eigenvalue와 matrix diagonalization에 관해 간략히 요약한 내용을 담고 있습니다.---
































참고 : 길버트 스트랭, 선형대수 입문 5판.
'NLP lab > 수학' 카테고리의 다른 글
| 로지스틱 일반화, 소프트맥스 유도하기 (3) | 2022.05.03 |
|---|---|
| 계산 그래프를 활용한 편미분 구하기, 역전파법 이해 (2) | 2022.02.08 |
