0. 계산 그래프를 이용해 편미분을 구하는 방법이란?
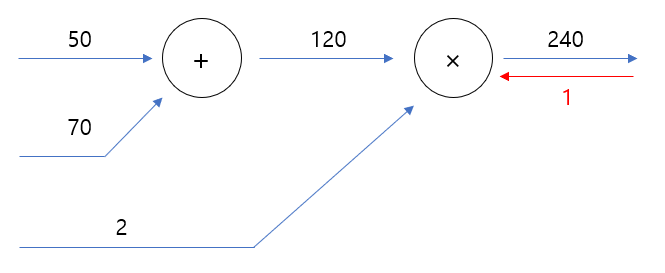
$$ z=(a+b) \cdot c|_{a=50, b=70, c=2} =240 $$
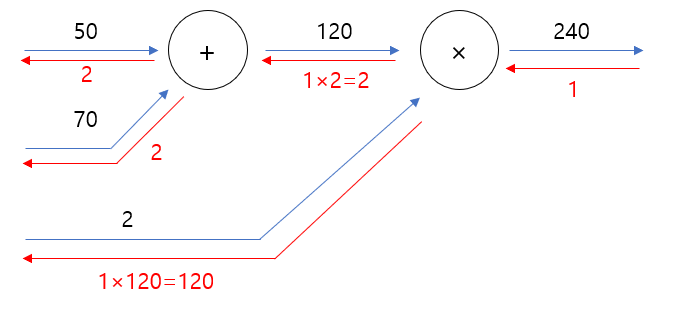
이 식을 위의 그림처럼 계산 그래프로 표현할 수 있다. 역전파법을 이용해서 편미분을 구하면
$$ \left.\frac{\partial z}{\partial a}\right|_{a=50, b=70, c=2}=2 $$
$$ \left.\frac{\partial z}{\partial b}\right|_{a=50, b=70, c=2}=2 $$
$$ \left.\frac{\partial z}{\partial c}\right|_{a=50, b=70, c=2}=120 $$
로 해석적으로 구한 해와 일치함을 확인할 수 있다.
왜 1부터 시작하는지, 왜 덧셈은 그냥 흐르고 곱셈은 반대쪽 라인의 값을 곱해주면 되는지, 원리를 이해하고 분수함수 등에도 적용해보자. 나아가 다변수함수의 편미분과 복잡한 함수의 편미분 구하기에도 적용해보자.
1. Chain rule을 계산 그래프에 적용
계산 그래프로 미분을 계산하는 아이디어의 시작을 다음 그림으로부터 알아보자.
$$ \frac{\partial z}{\partial x}=\frac{\partial z}{\partial y}\frac{\partial y}{\partial x} $$
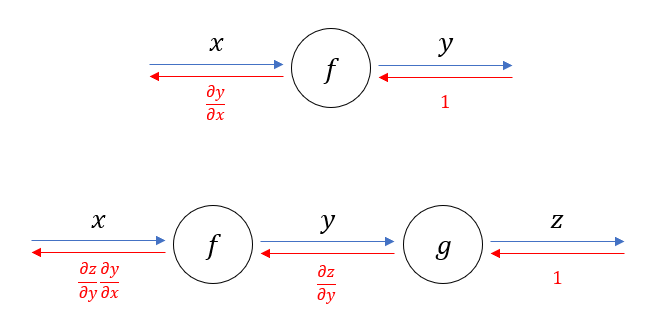
역전파법을 시작할 때 맨 오른쪽 빨간 화살표가 1부터 시작하는 이유는, 상수함수의 미분이 1이기 때문이다. 만약 이 함수로 계산이 끝나지 않고 다음 함수가 쭉 이어진다면, (예를 들어 \( L(g(f(x))) \) ) 1로 시작하지 않고 \( \frac{\partial L}{\partial z} \) 로 시작할 수 있다. \( L \) 을 쓴 이유는 보통 손실 함수(Loss function)가 맨 뒤에 오기 때문이다.
2. 특정한 값에서의 편미분 찾기
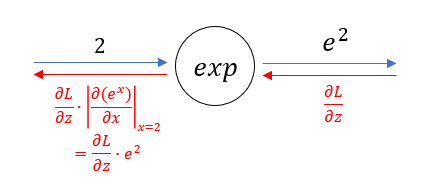
☆절댓값 기호가 아니라 안의 식에 x=2를 대입하라는 기호!★
딥러닝 구현시에는 편미분의 해석적 식이 아니라 특정한 값에서의 미분값(또는 gradient)가 필요하다. 밑이 e인 지수함수에서의 x=2일 때의 미분값은 \( e^2 \) 이다. 그러므로 이걸 \( \frac{\partial L}{\partial z} \) 에 곱해주면 그림처럼 미분값을 얻을 수 있다.
다른 예시를 보자. \( z=xy \) 라는 함수가 있고 \( x=2, y=3 \) 일 때의 각각 편미분을 구해보자. 이번엔 손실 함수가 없다고 생각하고 1부터 시작한다.
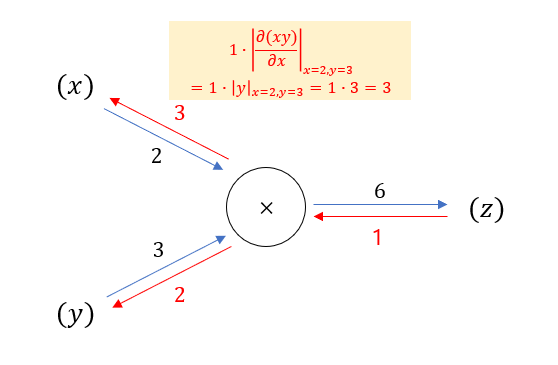
두 번째 예시에서 \( z \) 의 \( x \) 에 대한 편미분을 구하고 싶어서, 시작값인 1에 z의 x에 대한 편미분에 x=2, y=3을 대입한 값인 3을 곱해서 3이 나왓다.
어떤 노드를 지날 때, 그 노드가 의미하는 함수의 편미분에 입력값을 대입한 값을 곱해주면 된다.
그래서 역전파법을 할 때 이항 연산인 곱셈에서는 반대쪽 라인의 값을 곱해준 것이다.
마찬가지 방법으로 덧셈 연산 노드에서 미분값이 변하지 않는 이유도 확인할 수 있다.
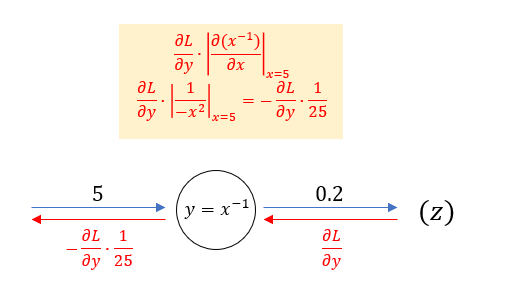
분수함수 \( y=\frac{1}{x} \) 노드에서의 역전파법 예시를 마지막으로 들어보자.
복잡한 다변수함수의 편미분도 계산해보자.
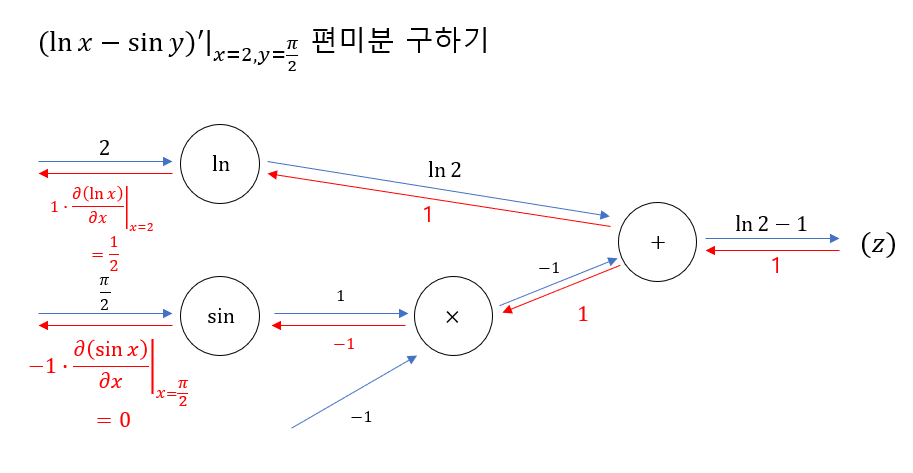
$$ \frac{\partial z}{\partial x}=\frac{1}{2} $$
$$ \frac{\partial z}{\partial x}=0 $$
임을 계산할 수 있다.
3. 복잡한 함수를 하나의 노드로 퉁쳐보자
위의 예시를 해보면서 어떤 노드가 수행하는 함수를 미분만 할 수 있으면 편미분을 구할 수 있음을 알았다. 그렇다면 다음 함수를 하나의 노드라고 생각해보자.
$$ sigmoid(x)=\frac{1}{1+e^{-x}} $$
이번엔 \( x \) 에 특정한 값을 넣지 않고 그냥 \( x \)로 두었다.
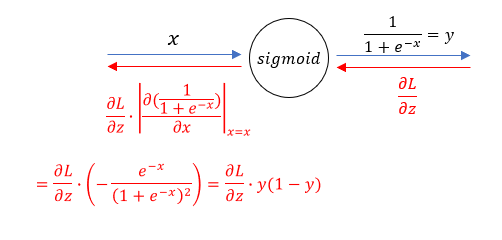
이렇게 exp, +, × 등의 노드를 여러 개 쓰지 않고도 노드 하나만으로 효율적으로 표현할 수 있다.
(특이한 점) sigmoid 함수에서는 출력값을 y라고 하면 미분값을 y만 가지고 표현할 수 있다.
4. sigmoid 함수를 파이썬으로 구현
다음은 sigmoid 함수 layer를 파이썬으로 forward, backward 계산할 수 있게 구현한 코드이다.
class Sigmoid:
def __init__(self):
self.output = None
def forward(self, x):
self.output = 1 / (1 + np.exp(-x))
return output
def backward(self, d):
return d * (1.0 - self.output) * self.output
'NLP lab > 수학' 카테고리의 다른 글
| 로지스틱 일반화, 소프트맥스 유도하기 (3) | 2022.05.03 |
|---|---|
| 선형대수 복습 (0) | 2022.01.09 |
0. 계산 그래프를 이용해 편미분을 구하는 방법이란?


$$ z=(a+b) \cdot c|_{a=50, b=70, c=2} =240 $$
이 식을 위의 그림처럼 계산 그래프로 표현할 수 있다. 역전파법을 이용해서 편미분을 구하면
$$ \left.\frac{\partial z}{\partial a}\right|_{a=50, b=70, c=2}=2 $$
$$ \left.\frac{\partial z}{\partial b}\right|_{a=50, b=70, c=2}=2 $$
$$ \left.\frac{\partial z}{\partial c}\right|_{a=50, b=70, c=2}=120 $$
로 해석적으로 구한 해와 일치함을 확인할 수 있다.
왜 1부터 시작하는지, 왜 덧셈은 그냥 흐르고 곱셈은 반대쪽 라인의 값을 곱해주면 되는지, 원리를 이해하고 분수함수 등에도 적용해보자. 나아가 다변수함수의 편미분과 복잡한 함수의 편미분 구하기에도 적용해보자.
1. Chain rule을 계산 그래프에 적용
계산 그래프로 미분을 계산하는 아이디어의 시작을 다음 그림으로부터 알아보자.
$$ \frac{\partial z}{\partial x}=\frac{\partial z}{\partial y}\frac{\partial y}{\partial x} $$

역전파법을 시작할 때 맨 오른쪽 빨간 화살표가 1부터 시작하는 이유는, 상수함수의 미분이 1이기 때문이다. 만약 이 함수로 계산이 끝나지 않고 다음 함수가 쭉 이어진다면, (예를 들어 \( L(g(f(x))) \) ) 1로 시작하지 않고 \( \frac{\partial L}{\partial z} \) 로 시작할 수 있다. \( L \) 을 쓴 이유는 보통 손실 함수(Loss function)가 맨 뒤에 오기 때문이다.
2. 특정한 값에서의 편미분 찾기

☆절댓값 기호가 아니라 안의 식에 x=2를 대입하라는 기호!★
딥러닝 구현시에는 편미분의 해석적 식이 아니라 특정한 값에서의 미분값(또는 gradient)가 필요하다. 밑이 e인 지수함수에서의 x=2일 때의 미분값은 \( e^2 \) 이다. 그러므로 이걸 \( \frac{\partial L}{\partial z} \) 에 곱해주면 그림처럼 미분값을 얻을 수 있다.
다른 예시를 보자. \( z=xy \) 라는 함수가 있고 \( x=2, y=3 \) 일 때의 각각 편미분을 구해보자. 이번엔 손실 함수가 없다고 생각하고 1부터 시작한다.

두 번째 예시에서 \( z \) 의 \( x \) 에 대한 편미분을 구하고 싶어서, 시작값인 1에 z의 x에 대한 편미분에 x=2, y=3을 대입한 값인 3을 곱해서 3이 나왓다.
어떤 노드를 지날 때, 그 노드가 의미하는 함수의 편미분에 입력값을 대입한 값을 곱해주면 된다.
그래서 역전파법을 할 때 이항 연산인 곱셈에서는 반대쪽 라인의 값을 곱해준 것이다.
마찬가지 방법으로 덧셈 연산 노드에서 미분값이 변하지 않는 이유도 확인할 수 있다.
분수함수 \( y=\frac{1}{x} \) 노드에서의 역전파법 예시를 마지막으로 들어보자.

복잡한 다변수함수의 편미분도 계산해보자.

$$ \frac{\partial z}{\partial x}=\frac{1}{2} $$
$$ \frac{\partial z}{\partial x}=0 $$
임을 계산할 수 있다.
3. 복잡한 함수를 하나의 노드로 퉁쳐보자
위의 예시를 해보면서 어떤 노드가 수행하는 함수를 미분만 할 수 있으면 편미분을 구할 수 있음을 알았다. 그렇다면 다음 함수를 하나의 노드라고 생각해보자.
$$ sigmoid(x)=\frac{1}{1+e^{-x}} $$
이번엔 \( x \) 에 특정한 값을 넣지 않고 그냥 \( x \)로 두었다.

이렇게 exp, +, × 등의 노드를 여러 개 쓰지 않고도 노드 하나만으로 효율적으로 표현할 수 있다.
(특이한 점) sigmoid 함수에서는 출력값을 y라고 하면 미분값을 y만 가지고 표현할 수 있다.
4. sigmoid 함수를 파이썬으로 구현
다음은 sigmoid 함수 layer를 파이썬으로 forward, backward 계산할 수 있게 구현한 코드이다.
class Sigmoid:
def __init__(self):
self.output = None
def forward(self, x):
self.output = 1 / (1 + np.exp(-x))
return output
def backward(self, d):
return d * (1.0 - self.output) * self.output
'NLP lab > 수학' 카테고리의 다른 글
| 로지스틱 일반화, 소프트맥스 유도하기 (3) | 2022.05.03 |
|---|---|
| 선형대수 복습 (0) | 2022.01.09 |
